
- はじめに
- 1次元ランダムウォーク
- 2次元ランダムウォーク: 2方向移動
- 2次元ランダムウォーク: 全方向移動
- ランダムウォークで画像表示のアニメーションを作成してみると、こうなる。
- twitterから収集した画像を使ってみたら、こうなる。
- まとめ
- 参考資料
はじめに
ランダムウォークと聞いて、その響からも、皆さん、さぞ憧れのところでしょうか。
ランダムウォークとは、英語で書くとRandom walkで、次に進む位置が確率的に無作為(ランダム)に決定される運動のことを指します。
もう少し、噛み砕いて言うと、、ランダムにガチャガチャっと動くやつってことです。高校物理で習ったような、ブラウン運動のモデルでもあります。
この記事では、1次元と2次元のランダムウォークについて紹介します。
ランダムウォークをどう利用するか??ということで、、最後に、 Google検索などで取得した画像にランダムウォークでモーションをつけて可視化してみたいと思います。
それでは、始めましょう。
実行環境
以下が、実行環境です。
実行環境 macOS Big Sur (バージョン11.5.2) MacBook Air (M1, 2020) チップ Apple M1 メモリ 16GB
パッケージ準備
今回使用する、Rパッケージを準備します。
#パッケージ・インストール pack <- c("GoogleImage2Array", "animation", "ggplot2", "gganimate", "rtweet", "tidyverse") install.packages(pack[!(pack %in% unique(rownames(installed.packages())))]) #ロード for(n in 1:length(pack)){ eval(parse(text = paste0("library(", pack[n], ")"))) }; rm("n", "pack")
1次元ランダムウォーク
まずは、1次元のランダムウォークを解説します。この運動は、1つの軸上を前後に移動するので、試行回数で展開して挙動を見てみます。
シンプルな実行例としては、-1(後進)あるいは1(前進)をランダムサンプリングするということを、N回試行した後に、cumsum関数で、累積和を求める方法です。また、ランダムサンプリングには、sample関数を使用します。
また、類似のことは、stats::arima.sim関数でもできるようです。今回は、割愛します。
では、実行してみます。
#乱数生成: 省略可 set.seed(123) #試行回数の設定 n <- 1000 #実行: 初期位置として、最初の0はあった方が良い x <- c(0, cumsum(sample(c(-1, 1), size=n, replace=TRUE))) #プロット plot(x, type="l")
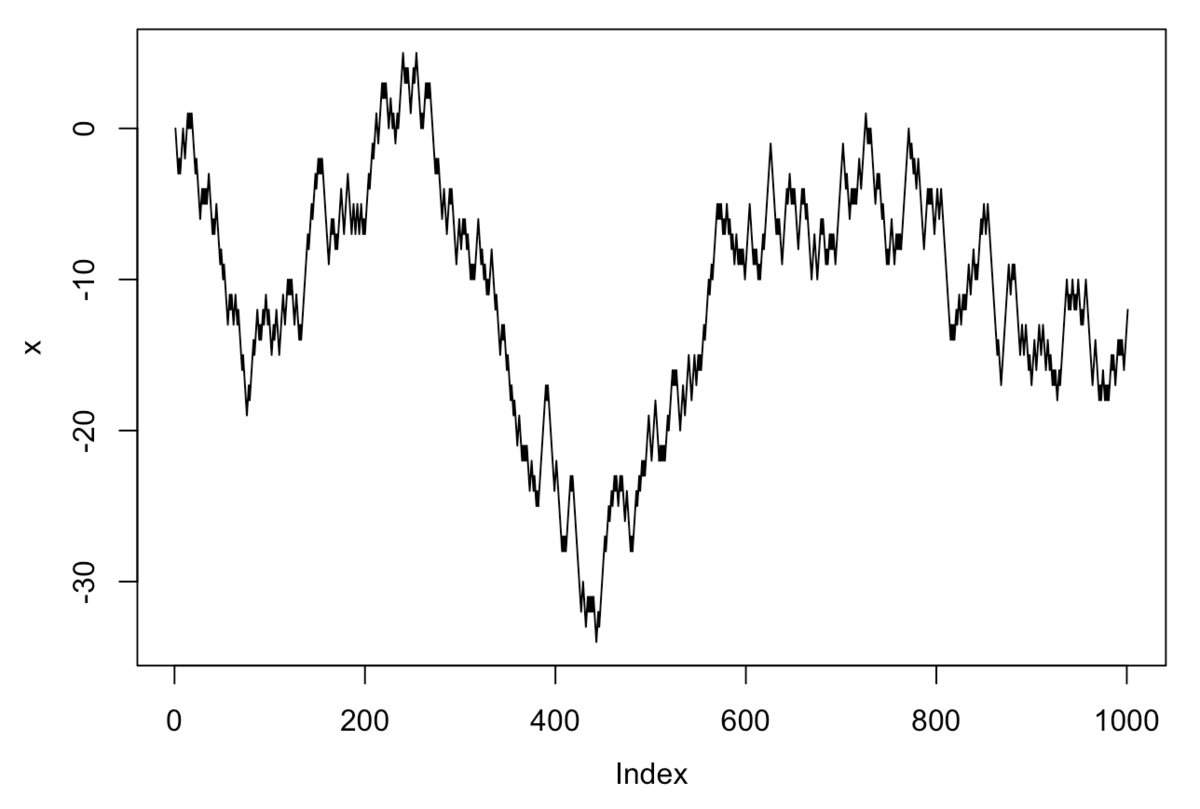
1つだけではなくて、続いて、複数の一次元のランダムウォークを生成してみます。
#空変数の作成 X <- c() #試行回数の設定 n <- 1000 #実行 for(i in 1:10){ #ランダムウォーク生成 x <- c(0, cumsum(sample(c(-1, 1), size=n, replace=TRUE))) #列結合 X <- cbind(X, x) } #表示 head(X) # x x x x x x x x x x #[1,] 0 0 0 0 0 0 0 0 0 0 #[2,] 1 1 1 1 1 1 1 1 -1 -1 #[3,] 2 0 0 0 2 0 0 2 -2 0 #[4,] 3 -1 1 1 3 -1 1 3 -3 -1 #[5,] 4 -2 0 2 2 -2 0 4 -4 -2 #[6,] 3 -1 1 1 3 -1 1 3 -5 -3 #プロット par(mgp=c(2.5, 1, 0)) matplot(X, type="l", lty=1, xlab="Number of trials", col = rainbow(10, alpha = 0.6))

このように試行ごとで、全然パターンが違うというのは、やはり興味深いですね。
次に、これをアニメーション表示してみます。
1000回分の試行をすべてアニメーションにすると、冗長なのとサイズが大きくなるので、初めの100回分のみで、アニメーションを作成してみました。
#試行回数の制限 k <- 100 #アニメーション作成 animation::saveGIF({for(i in 2:k){ matplot(c(1:nrow(X))[1:i], X[1:i,], type="l", lty=1, lwd=1.5, col=rainbow(ncol(X), alpha = 0.5), xlab="Number of trials", ylab="", xlim=c(0, k), ylim=c(min(X[1:k,]), max(X[1:k,])), cex.lab=1.2, cex.axis=1.2) matpoints(t(rep(i, ncol(X))), t(X[i,]), pch=16, col=rainbow(ncol(X), alpha = 0.7), cex=1.25) }}, movie.name = "01_motion.gif", interval = 0.1, nmax = k, ani.width = 500, ani.height = 500, dpi=500)

次に、ggplotで作図する場合には、データセットの形式を少し変える必要があります。
#空変数の作成 X <- c() #試行回数の設定 n <- 1000 #10回の繰り返し実行 for(i in 1:10){ #ランダムウォーク生成 x <- c(0, cumsum(sample(c(-1, 1), size=n, replace=TRUE))) #DF作成 x1 <- data.frame(trials=0:n, x=x, sim=i) #行結合 X <- rbind(X, x1) } #表示 head(X) # trials x sim #1 0 0 1 #2 1 -1 1 #3 2 0 1 #4 3 1 1 #5 4 2 1 #6 5 3 1 #プロット ggplot(data = X, aes(x = trials, y = x, color = factor(sim))) + geom_line(alpha = 0.6) + theme(legend.position = "none")
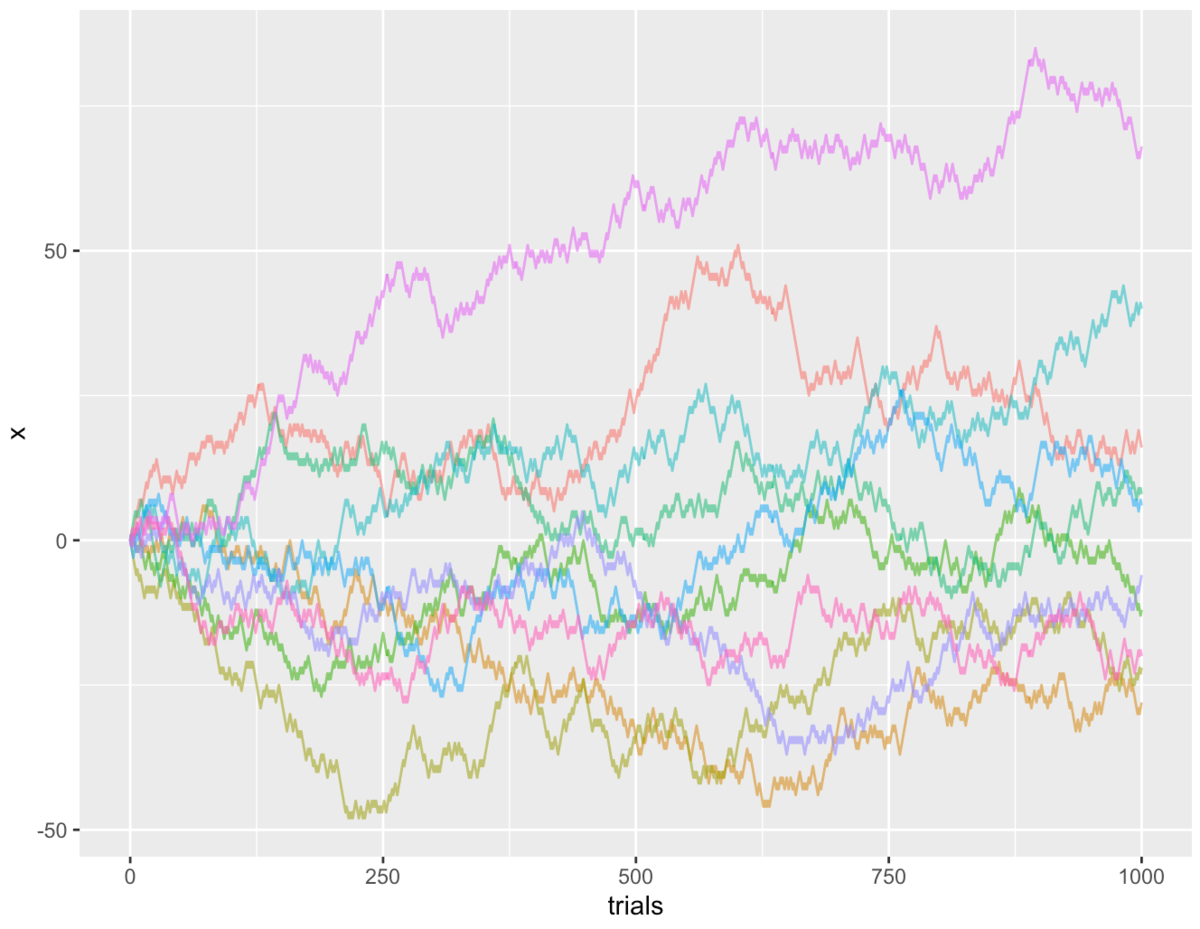
2次元ランダムウォーク: 2方向移動
次に、2次元のランダムウォークでは、2方向と全方向の移動を考慮します。
まず、2方向移動は、x軸あるいはy軸の方向にランダムウォークで移動するというものです。
その為、x軸あるいはy軸の方向に前進するか、後進するかをその時その時にランダムで決定されます。
では、実行してみます。
#試行回数の設定 n <- 1000 #実行(1) x <- sample(c(-1, 1), size=n, replace=TRUE) #実行(2) y <- sample(c("x", "y"), size=n, replace=TRUE) #DF作成 Dat <- data.frame(trials=0:n, x=0, y=0) #xあるいはy列に割り振る for(i in 1:n){ Dat[c(i+1),y[i]] <- x[i] } #累積計算 Dat$cx <- cumsum(Dat$x) Dat$cy <- cumsum(Dat$y) #表示 head(Dat) # trials x y cx cy #1 0 0 0 0 0 #2 1 -1 0 -1 0 #3 2 0 -1 -1 -1 #4 3 0 -1 -1 -2 #5 4 1 0 0 -2 #6 5 0 -1 0 -3 #プロット plot(Dat$cx, Dat$cy, type="l", xlab="x", ylab="y")
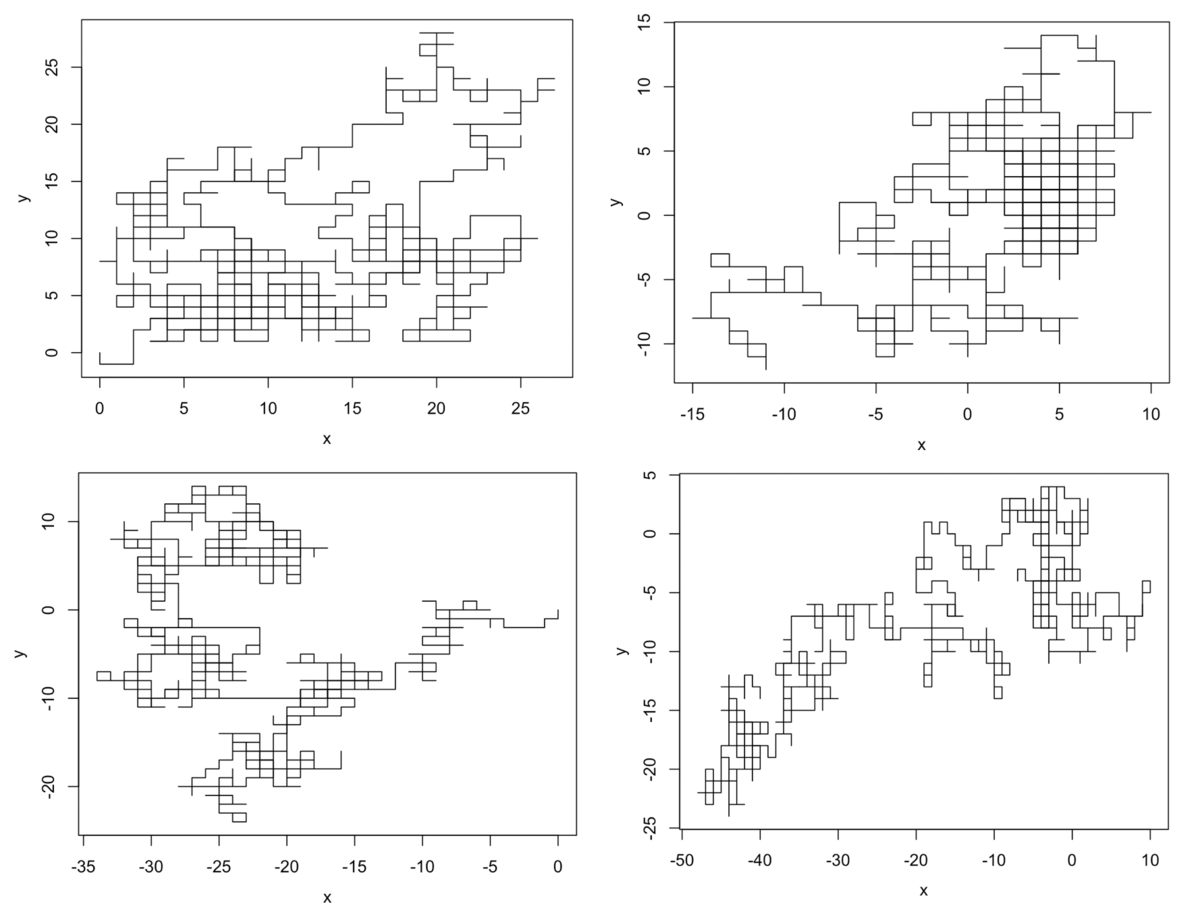
何度か実行してみたところ、ヘンテコな幾何学模様が沢山生成されますね。
2次元ランダムウォーク: 全方向移動
次に、全方向移動に移動する場合のランダムウォークを検討します。
この場合には「0から2π(パイ)」の間の一様乱数を生成します。
実際のやり方としては、runif関数で、0から1の間の離散型一様分布の乱数を発生させて、2π、Rでの記法は2*piで補正します。
#試行回数の設定 n <- 1000 #ランダムに値を生成 r_vec <- 2 * pi * runif(n = n, min = 0, max = 1) #DF作成 Dat <- data.frame(trials=0:n, x=0, y=0) #集計 Dat$x[2:nrow(Dat)] <- cumsum(cos(r_vec)) Dat$y[2:nrow(Dat)] <- cumsum(sin(r_vec)) #表示 head(Dat) # trials x y #1 0 0.0000000 0.00000000 #2 1 0.9454171 0.32586263 #3 2 1.7773490 0.88074037 #4 3 1.1780515 0.08021397 #5 4 1.0230444 1.06812733 #6 5 2.0069765 0.88958413 #プロット plot(Dat$x, Dat$y, type="l", xlab="x", ylab="y")
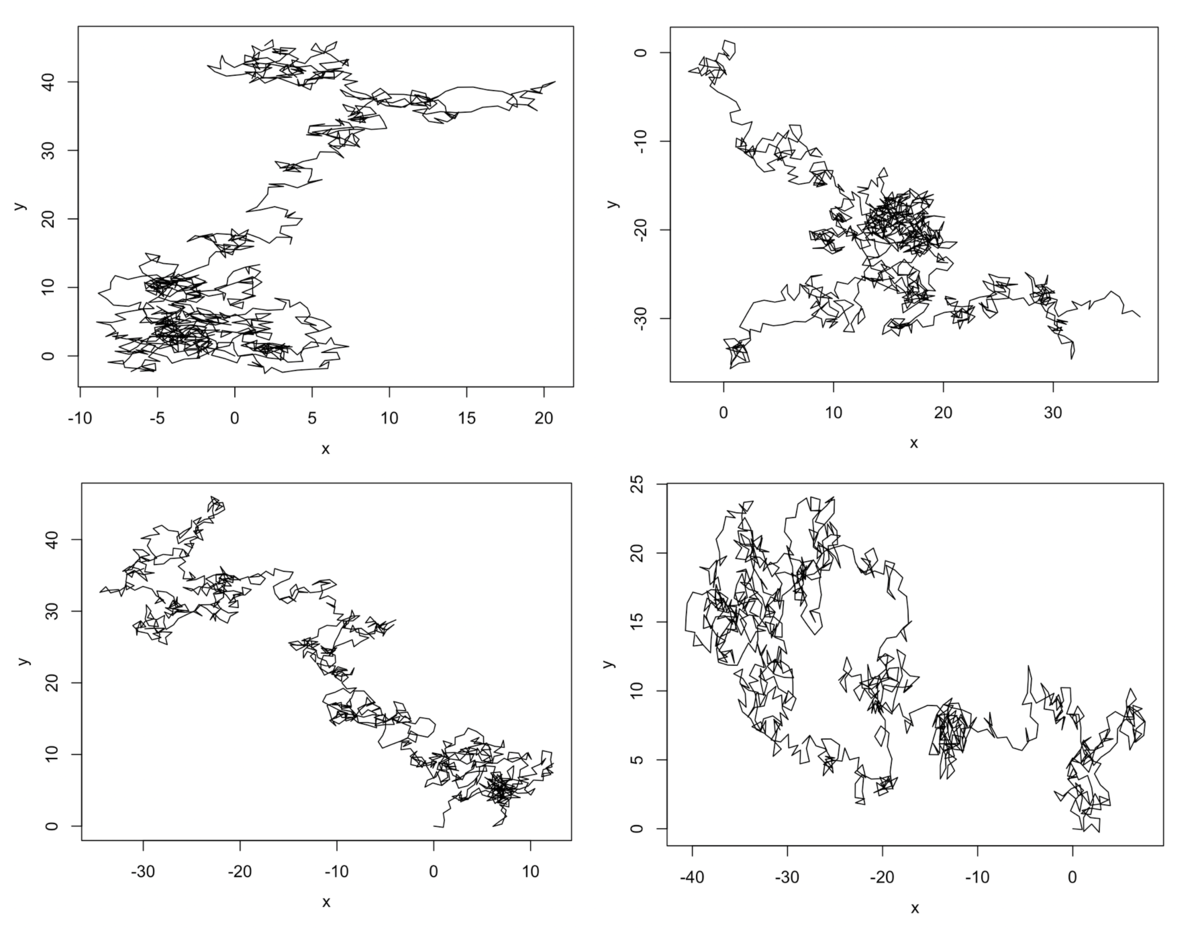
何度か実行してみたところ、ガチャガチャしてて、ランダムウォークっぽい感じですね。
続いて、複数の二次元のランダムウォークを生成してみます。
#試行回数の設定 n <- 200 #空変数 Z <- c() #20回の繰り返し実行 for(i in 1:20){ #ランダムに値を生成 r_vec <- 2 * pi * runif(n = n, min = 0, max = 1) #DF作成 Dat <- data.frame(trials=0:n, x=0, y=0) #集計 Dat$x[2:nrow(Dat)] <- cumsum(cos(r_vec)) Dat$y[2:nrow(Dat)] <- cumsum(sin(r_vec)) #シミュレーション回数 Dat$sim <- i #行結合 Z <- rbind(Z, Dat) } #表示 head(Z) # trials x y sim #1 0 0.0000000 0.0000000 1 #2 1 0.8785386 0.4776714 1 #3 2 1.3394305 1.3651277 1 #4 3 2.3038196 1.6296150 1 #5 4 3.2821351 1.4224948 1 #6 5 3.2640218 0.4226589 1 #プロット ggplot(data = Z, aes(x = x, y = y, color=factor(sim))) + geom_path(alpha = 0.6) + theme(legend.position = "none") #注釈: geom_lineではなく、geom_pathを使用すること。

それでは、ggplot2のアニメーションも以下のように実行できます。
#アニメーション作図 p <- ggplot(Z, aes(x = x, y = y, color=factor(sim))) + geom_point(size = 4, show.legend = F) + geom_path(size = 1, alpha = 0.5) + gganimate::transition_reveal(along = trials) + coord_fixed(ratio = 1) + labs(title = "2D Random Walk", subtitle = "Trials: {frame_along}") #実行: 40秒くらいかかる p #gif画像の出力: 実行時間 60秒くらい gganimate::animate(p, nframes=max(Z$trials)+1, fps = 10, width = 500, height = 500, renderer = gganimate::gifski_renderer("02_motion.gif"))

ランダムウォークで画像表示のアニメーションを作成してみると、こうなる。
早速、画像を準備します。
それでは、GoogleImage2array関数を使って、Google画像検索をして、猫の画像を取得します。
次に、その画像を使って、アニメーションを作成したいと思います。
#「猫」画像の取得 CatImg <- GoogleImage2array("猫", gl="ja") #画像表示 display.array(CatImg)

こういう、猫の画像です。
続いて、先程の2次元のランダムウォークの結果を使って、 猫画像それぞれをrasterImage関数で作図してみます。
#実行 animation::saveGIF({for(l in 1:(max(Z$trials)+1)){ #空プロットの作成 plot(Z[,2], Z[,3], type="n", axes = FALSE, xlab="", ylab="") #線の作図 for(m in 1:max(Z$sim)){ Z1 <- Z[Z$sim == m,] lines(x = Z1$x[1:l], y = Z1$y[1:l], col=rainbow(max(Z$sim), alpha = 0.7)[m]) } #画像サイズのパラメータ計算(6%) a1 <- diff(range(Z[,2]))*0.06 b1 <- diff(range(Z[,3]))*0.06 #ラスター画像をプロット for(n in 1:dim(CatImg$array)[1]){ ff <- t(as.raster(CatImg$array[n,,,])) ZZ <- Z[Z$sim == n,] rasterImage(ff, ZZ[l,2]-a1, ZZ[l,3]-b1, ZZ[l,2]+a1, ZZ[l,3]+b1) }}}, movie.name = "03_motion.gif", interval = 0.1, nmax = max(Z$trials)+1, ani.width = 600, ani.height = 600, dpi=500)

さてさて、こう言う感じになります。
実際、ani.width = 1000, ani.height = 1000, dpi=600に変更すると、サイズが27MBくらいになりますが、見易い解像度になります。
ブログにはアップできないのですが、、こちらにアップしています。
twitterから収集した画像を使ってみたら、こうなる。
では、続いて、twitterから収集した画像でもやってみましょう。
クエリは「猫島」にしました。 クエリオプションとして指定した、"filter:media"でメディアを含むツイートだけに(ほぼ?)絞れます。 また、"include_rts = TRUE"では、リツイートも検索に含められます。
また、ライブラリのバージョン(現在"rtweet v1.0.2"を使用)に寄るのか、URL情報は、他の方の記事とはやや違うロケーションに格納されている感じでした。
#検索 tweets <- search_tweets(q="猫島 filter:media", n = 200, include_rts = TRUE) #urlを収集 url <- c() for(n in 1:nrow(tweets)){ #n <- 1 a <- tweets$entities[[n]]$media$media_url b <- a[!is.na(a)] if(any(!is.na(b))){ url <- c(url, b) } } #重複を除く url2 <- unique(url) #ダウンロード関数の定義 dl_url <- function(dat){ download.file(dat, destfile = basename(dat), mode ="wb") Sys.sleep(0.5) } #ダウンロード実行! #url2[1:20] %>% walk(dl_url) #画像読み込み: ここではEBImageを使います Img <- c() for(j in 1:20){ a <- EBImage::resize(EBImage::readImage(url2[j]), w=64, h=64) Img <- EBImage::abind(Img, a, along=4) } #attrのdimnames属性を消す attr(Img, "dimnames") <- NULL #詳細表示 str(Img) #num [1:64, 1:64, 1:3, 1:20] 0.101 0.1941 0.0994 0.1437 0.1112 ...
画像はアレイ形式として、重ねていきます。
ちなみに、walk関数というのを初めて知りましたが、こう使うんですね。
続いて、アニメーションを作成します。
#アニメーション実行 animation::saveGIF({for(l in 1:(max(Z$trials)+1)){ #空プロットの作成 plot(Z[,2], Z[,3], type="n", axes = FALSE, xlab="", ylab="") #線の作図 for(m in 1:max(Z$sim)){ Z1 <- Z[Z$sim == m,] lines(x = Z1$x[1:l], y = Z1$y[1:l], col=rainbow(max(Z$sim), alpha = 0.7)[m]) } #画像サイズのパラメータ計算(6%) a1 <- diff(range(Z[,2]))*0.06 b1 <- diff(range(Z[,3]))*0.06 #ラスター画像をプロット for(n in 1:dim(Img)[4]){ ff <- t(as.raster(Img[,,,n])) ZZ <- Z[Z$sim == n,] rasterImage(ff, ZZ[l,2]-a1, ZZ[l,3]-b1, ZZ[l,2]+a1, ZZ[l,3]+b1) }}}, movie.name = "04_motion.gif", interval = 0.1, nmax = max(Z$trials)+1, ani.width = 1000, ani.height = 1000, dpi=600)
実際、こうなりました。じゃーん、、、解像度ワル!!

まとめ
ランダムウォークを見ていると、ココロが落ち着くところがありますね。 ヒトの中にも、類似する、ランダム性があるのでしょうね。
あと、Rでの簡易プロットの場合には、タンパク質の立体構造を線図にしたときと、ほぼ同じに見てますね。