京橋のバイオインフォマティシャンの日常

南国のビーチパラソルの下で、Rプログラムを打ってる日常を求めて、、Daily Life of Bioinformatician in Kyobashi of Osaka

【R言語での画像処理シリーズ（その２）】主成分分析(PCA)を用いて、画像特徴の次元圧縮をやってみた件

Mac R言語 R - EBImage 画像処理 R - 画像処理 R - 画像解析 主成分分析 KL変換 R - PCA R - 主成分分析/PCA 画像データ 2D画像 Wikipedia R - BiocManager R - EBImage.display R - EBImage::readImage R - quartz.save 次元圧縮 R - 次元圧縮 画像特徴量 par - family日本語設定

序章

今回は、Karhunen-Loève変換(KL変換)という手法を使って、 ヒマワリ画像の圧縮を行ってみた*1。

この手法のデフォルトでは、 主成分分析(PCA; Principal Component Analysis)をクロップ画像に適用することで、一度、画像を主成分ベクトルに変換する。 その後、第１～第(p/2)次元の主成分だけを使って、画像を再構成して(PCAの逆計算)、画像の圧縮を行う。

今回使用するヒマワリ画像は、RGB画像である。RGB画像は、R環境で読み込むと、[X, Y, 3]の３次元アレイ(配列)データとして扱われる。Red、Green、Blueがそれぞれ行列データとして扱われ、３次元空間でRGBのピクセル値が表される。

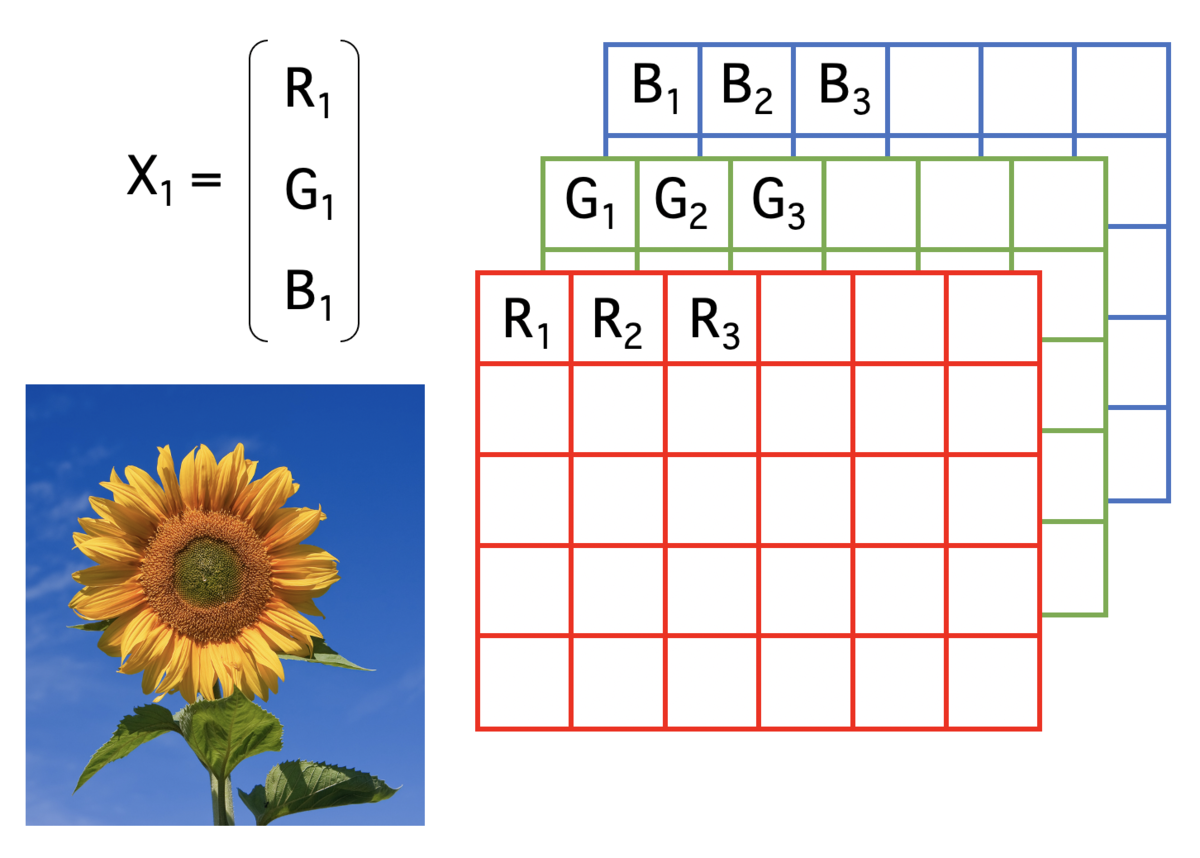
１つの手順として、入力画像をバッチに分割して、 バッチ画像内の画素値をラスタ順に並べて、ベクトル化する。 そのベクトルを積み重ねて、行列のデータセットを作成する。

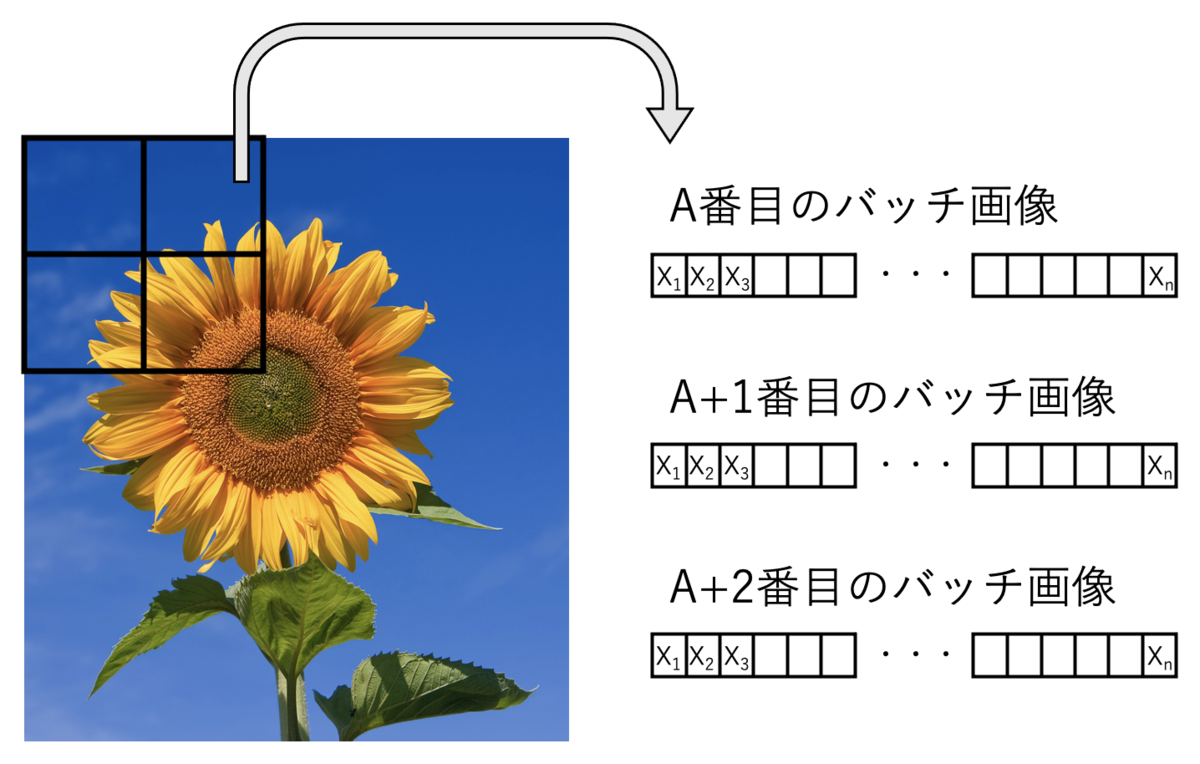
画像をどのくらいのサイズのバッチに分けるか?とか、 何次元までの主成分を用いるか?といったことがポイントになりそうである。

以下に、Rで実際の処理を行ってみた。

関連パッケージのインストール

#EBImageのインストール
install.packages("BiocManager")
BiocManager::install("EBImage", force = TRUE)

#explor & scatterplot3d & animationのインストール
install.packages(c("explor", "scatterplot3d", "animation"))

#ロード
library(EBImage)
library(explor)
library(scatterplot3d)
library(animation)

前回の記事も参照のこと。

skume.net

ひまわり画像をwikipediaからダウンロードして表示する

download.file関数を使って、Wikipediaからヒマワリの画像をダウンロードする。

そして、EBImageの関数群(readImage & display)を使って、読み込みと表示を行う。

#画像のダウンロード
download.file(url = "https://upload.wikimedia.org/wikipedia/commons/4/40/Sunflower_sky_backdrop.jpg", 
              destfile = "sunflower.jpg")

#画像の読み込み
library(EBImage); options(EBImage.display = "raster")
Img <- EBImage::readImage(files="./sunflower.jpg", type = "jpg")

#1024x1024にリサイズ
Img <- EBImage::resize(Img, w = 1024, h = 1024, filter="bilinear")

#画像の表示
EBImage::display(Img)
#quartz.save("Img01_sun.png", type="png", dpi=100); dev.off()

Imageクラスを「行列」に変換する

次に、前処理として、 ImageクラスのRGB画像をアレイ(配列)に変換する。 そして、RGBの各成分をベクトル化してから、 RGBの成分を行要素に持つ「行列」に変換する。

#クラス表示
str(Img)
#Formal class 'Image' [package "EBImage"] with 2 slots
#  ..@ .Data    : num [1:1024, 1:1024, 1:3] 0.003922 0.006104 0.0069 0.000713 0.002627 ...
#  ..@ colormode: int 2
#  ..$ dim: int [1:3] 1024 1024 3

#アレイに変換
ImgA <- array(Img, dim=dim(Img))
unlist(ImgA)[1:10]
# [1] 0.0039215686 0.0061044730 0.0068998412 0.0007129333 0.0026271446
# [6] 0.0039215686 0.0039215686 0.0031252281 0.0000000000 0.0015261519

# 行列に変換
ImgDat <- matrix(unlist(ImgA), ncol = dim(ImgA)[1]*dim(ImgA)[2], byrow = T)
ImgDat[,1:10]
#            [,1]        [,2]        [,3]         [,4]        [,5]
#[1,] 0.003921569 0.006104473 0.006899841 0.0007129333 0.002627145
#[2,] 0.278431373 0.280614277 0.281409645 0.2752227372 0.277136949
#[3,] 0.654901961 0.657084865 0.657880233 0.6516933254 0.653607537
#            [,6]        [,7]        [,8]      [,9]       [,10]
#[1,] 0.003921569 0.003921569 0.003125228 0.0000000 0.001526152
#[2,] 0.278431373 0.278431373 0.277635032 0.2745098 0.276035956
#[3,] 0.654901961 0.654901961 0.654105620 0.6509804 0.652506544

次に、行列の行要素を戻して、オリジナル画像と各RGB成分を表示させる。

#1枚目: Red成分の分離
ImgDat01 <- Img; ImgDat01[,,c(2:3)] <- 0
#2枚目: Green成分の分離
ImgDat02 <- Img; ImgDat02[,,c(1,3)] <- 0
#3枚目: Blue成分の分離
ImgDat03 <- Img; ImgDat03[,,c(1:2)] <- 0

#RGB成分を分離して表示する
EBImage::display(EBImage::combine(Img, ImgDat01, ImgDat02, ImgDat03),
                 nx=2, all=TRUE, spacing = 0.01, margin = 70)
#quartz.save("Img02_bunri.png", type="png", dpi=100); dev.off()

RGB成分を3D表示する

#データフレームの列要素に変換する
ImgDatRGB <- data.frame(R=as.vector(ImgDat01[,,1]),
                        G=as.vector(ImgDat02[,,2]),
                        B=as.vector(ImgDat03[,,3]))
dim(ImgDatRGB)
head(ImgDatRGB)

#図示
scatterplot3d::scatterplot3d(round(ImgDatRGB, 4), pch=20, color="blue", cex.symbols=0.1, 
                               xlab="R", ylab="G", zlab="B",box=F)
#quartz.save("Img03_3D.png", type="png", dpi=100); dev.off()

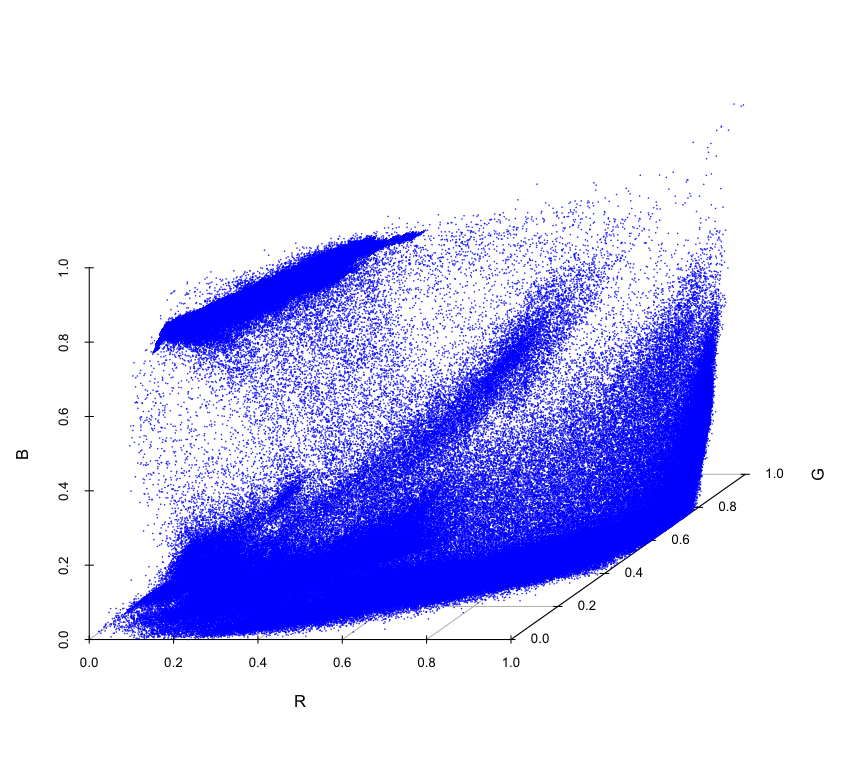
う〜ん、あんまりよく分からない。

ヒマワリ画像を64x64ピクセルでクロップ（分割）する

#パラメータ設定
k <- 64
m <- dim(Img)[1]/k
m1 <- c(1:m)*k - k + 1
m2 <- c(1:m)*k

#横方向の設定
w1 <- rep(m1, times = m)
w2 <- rep(m2, times = m)
#縦方向の設定
h1 <- rep(m1, each = length(m1))
h2 <- rep(m2, each = length(m2))
#ピクセス数
p0 <- length(m1)*length(m2)

#画像をCropして、ベクトルに変換して重ねていく。
ImgDatCrop <- c()
for(n in 1:c(m*m)){
  #n <- 2
  Crop01 <- unlist(ImgDat01[c(h1[n]:h2[n]),c(w1[n]:w2[n]),1])
  Crop02 <- unlist(ImgDat02[c(h1[n]:h2[n]),c(w1[n]:w2[n]),2])
  Crop03 <- unlist(ImgDat03[c(h1[n]:h2[n]),c(w1[n]:w2[n]),3])
  ImgDatCrop <- rbind(ImgDatCrop, c(Crop01, Crop02, Crop03))
}

#詳細
dim(ImgDatCrop)
#[1]   256 12288

ImgDatCrop[1:3,1:10]
#            [,1]        [,2]        [,3]         [,4]        [,5]
#[1,] 0.003921569 0.006104473 0.006899841 0.0007129333 0.002627145
#[2,] 0.023931956 0.026674185 0.027450980 0.0235294118 0.022355663
#[3,] 0.003193934 0.000000000 0.000000000 0.0000000000 0.000000000
#            [,6]        [,7]        [,8]       [,9]       [,10]
#[1,] 0.003921569 0.003921569 0.003125228 0.00000000 0.001526152
#[2,] 0.021938189 0.028931143 0.044128429 0.05367229 0.058823529
#[3,] 0.001536227 0.003921569 0.002798294 0.00000000 0.000000000

#クロップ画像の表示
par(mfcol = c(length(m1), length(m2)), mai = c(0.1, 0.1, 0.1, 0.1))
for(n in 1:p0){
a <- EBImage::Image(array(ImgDatCrop[n,], dim=c(k, k, 3)), colormode = "Color")
EBImage::display(EBImage::rotate(a, angle=0))  
}
#quartz.save("Img04.png", type="png", dpi=100); dev.off()
#saveRDS(ImgDatCrop, "ImgDatCrop.Rds")

このステップで、ベクトル画像を元の64x64画像に戻して、タイル状に表示した。

主成分分析(PCA)、累積寄与率の計算と可視化

続いて、クロップ画像の相関行列に対して、 PCAを実行して、累積寄与率などの計算や可視化を行う。

#再読み込みの場合
#ImgDatCrop <- readRDS("ImgDatCrop.Rds")

#次元数
dim(ImgDatCrop)

#Q-mode PCA: 相関行列
pca <- prcomp(ImgDatCrop, scale = TRUE)

#固有値(Standard deviation)、寄与率(Proportion of Variance)、累積寄与率(Cumulative Proportion)の表示
round(summary(pca)$importance, 2)[,1:10]
#                         PC1   PC2   PC3   PC4   PC5   PC6   PC7   PC8   PC9  PC10
#Standard deviation     77.00 44.76 25.62 17.82 16.24 14.03 13.58 12.42 11.47 11.01
#Proportion of Variance  0.48  0.16  0.05  0.03  0.02  0.02  0.01  0.01  0.01  0.01
#Cumulative Proportion   0.48  0.65  0.70  0.72  0.75  0.76  0.78  0.79  0.80  0.81

#主成分分析の主成分(固有ベクトル)の表示（一部）
round(pca$rotation, 3)[c(1:5),c(1:10)]
#      PC1   PC2    PC3   PC4    PC5    PC6    PC7    PC8   PC9  PC10
#[1,] 0.01 0.000 -0.012 0.008 -0.008 -0.006 -0.009 -0.011 0.003 -0.02
#[2,] 0.01 0.001 -0.012 0.009 -0.008 -0.007 -0.007 -0.009 0.000 -0.02
#[3,] 0.01 0.001 -0.012 0.009 -0.009 -0.008 -0.005 -0.008 0.001 -0.02
#[4,] 0.01 0.001 -0.012 0.008 -0.010 -0.008 -0.004 -0.009 0.002 -0.02
#[5,] 0.01 0.001 -0.012 0.009 -0.010 -0.006 -0.004 -0.011 0.002 -0.02

#主成分得点（一部）
round(pca$x, 3)[c(1:5),c(1:10)]
#         PC1     PC2    PC3    PC4   PC5    PC6    PC7    PC8    PC9  PC10
#[1,] -85.099 -41.512  6.937 -0.125 0.823 -0.755  0.065  0.894 -1.743 1.595
#[2,] -84.157 -37.342 -1.268 -0.003 3.570 -1.325  1.064  1.971  0.358 1.698
#[3,] -85.098 -33.581  3.612  0.768 2.403 -1.103  2.272  2.372 -2.263 1.970
#[4,] -70.808  -9.993 19.623 -1.219 0.390 -4.685 -1.409  1.029  3.036 0.987
#[5,] -67.116  -7.996 -0.804 -1.582 0.146  0.598 -2.740 -0.015  1.285 0.306

#Cumulative Proportion (累積寄与率)の計算
vars <- apply(pca$x, 2, var)
result <- cumsum(vars / sum(vars))

par(mgp=c(2.5, 1, 0), mai = c(0.75, 0.75, 0.2, 0.2))
plot(result, type="b", pch=4, col="skyblue",
     xlab="Principal Component", ylim=c(0,1),
     ylab="Cumulative proportion of variance explained",
     cex=0.5, cex.lab=0.9)
abline(h=0.8, col="red", lwd=0.5); abline(v=sum(result < 0.8)+1, col="blue", lty=2, lwd=0.5)
#quartz.save("Img05_CumulativeProportion.png", type="png", dpi=100); dev.off()

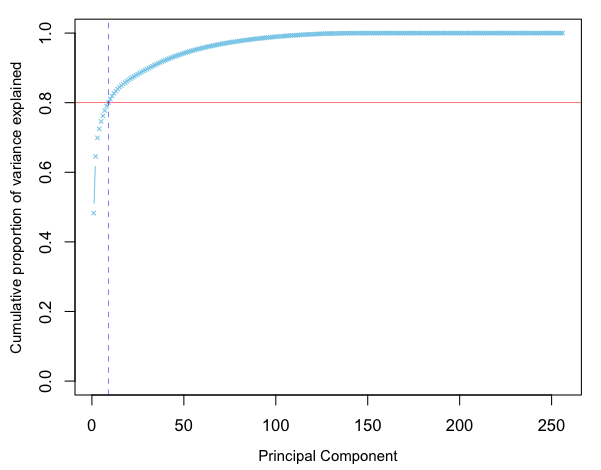
PCA結果のインタラクティブな可視化

explorパッケージは、解析結果探索のためのインターフェース を提供します。

explorを実行するとShinyアプリを起動して、 PCAの解析結果をインタラクティブに可視化・探索できます。

library(explor)

#インタラクティブ表示
explor::explor(pca)

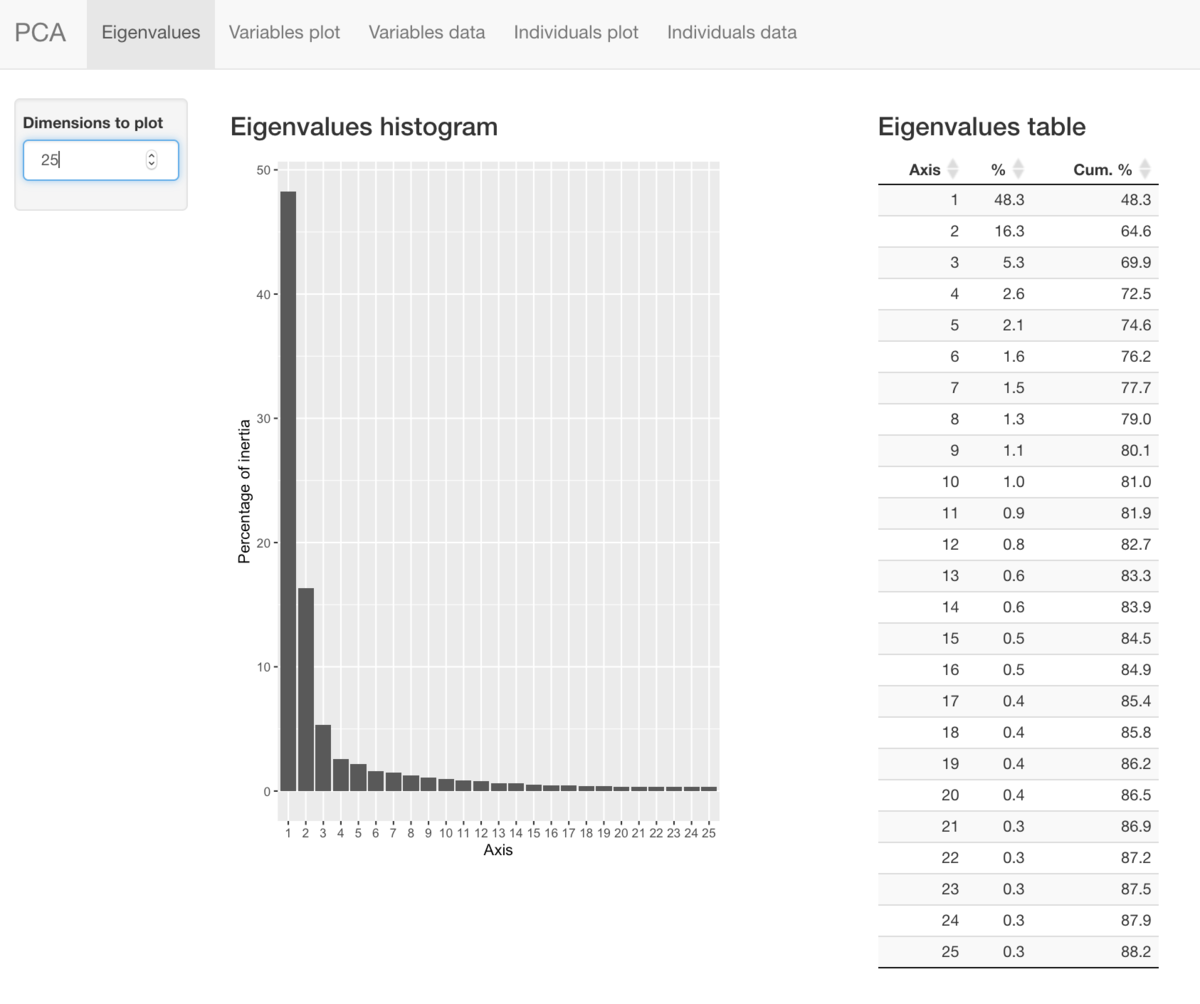
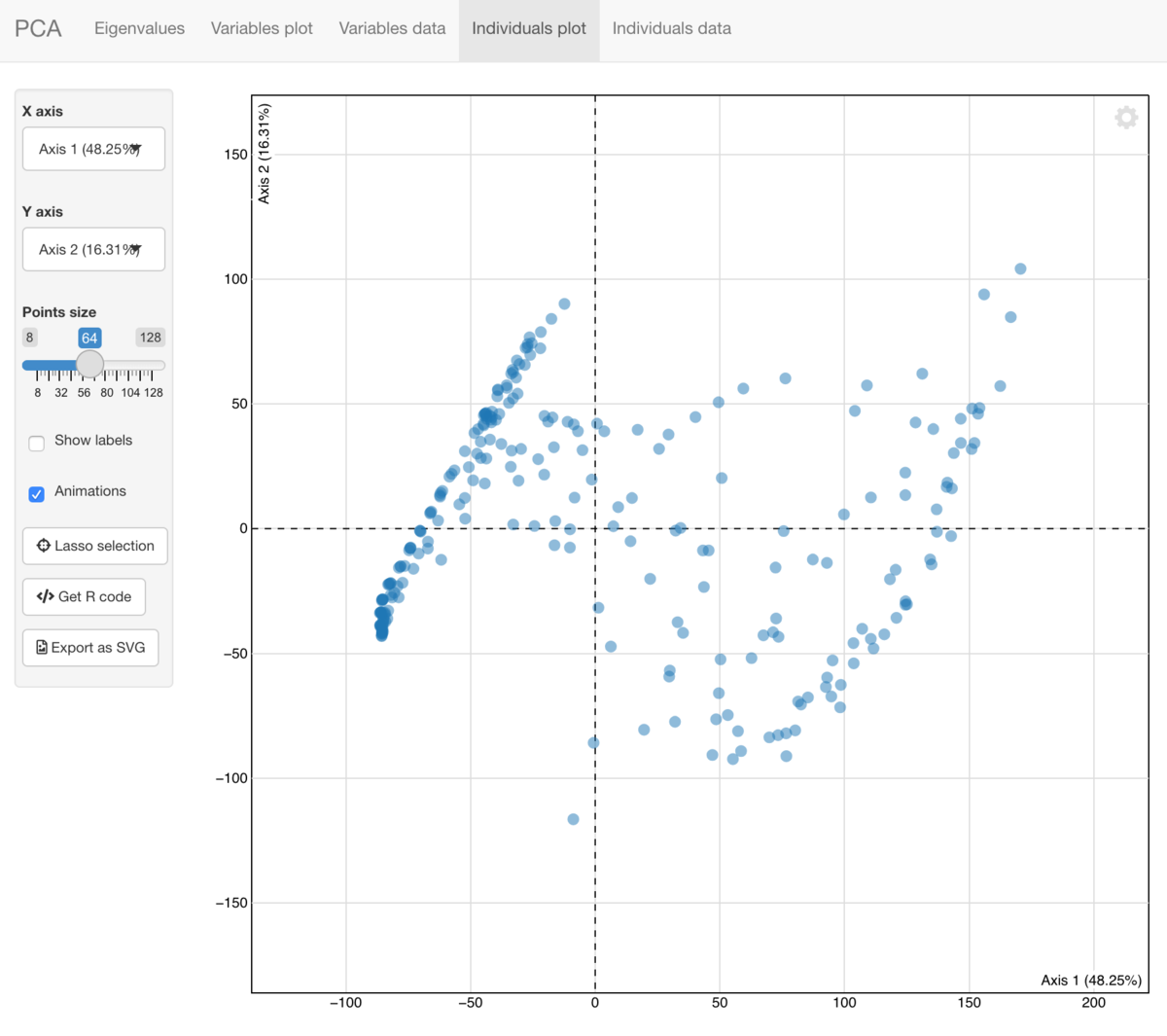
shinyを使うけど、これの可視化ツールは、結構便利かも。

主成分得点(Principal component score)の可視化

次に、主成分得点を二次元にマッッピングする。

#ロード
library(EBImage); options(EBImage.display = "raster")

#主成分得点: 元の情報から情報損失量を除いた、新しい情報量を意味する
pcaScore <- round(pca$x, 4)
str(pcaScore)
# num [1:256, 1:256] -85.1 -84.2 -85.1 -70.8 -67.1 ...
# - attr(*, "dimnames")=List of 2
#  ..$ : NULL
#  ..$ : chr [1:256] "PC1" "PC2" "PC3" "PC4" ...

#最小値を0、最大値を1とする正規化
pcaScore0 <- scale(pcaScore, center = apply(pcaScore, 2, min), scale = (apply(pcaScore, 2, max) - apply(pcaScore, 2, min)))

#displayでの作図
#b <- EBImage::Image(array(pcaScore0, dim=c(p0, p0, 1)), colormode = "Grayscale")
#EBImage::display(EBImage::rotate(b, angle=0)) 

#imageでの作図
par(mgp=c(1, 1, 0), cex=1.25)
graphics::image(x=1:p0, y=1:p0, z=matrix(rev(unlist(pcaScore0[,-p0])), nrow = 256, byrow = F),
                 xaxt = "n", yaxt = "n", xlab="PC (1-256)", ylab="Components")
#quartz.save("Img06_pcaScore0.png", type="png", dpi=100); dev.off()

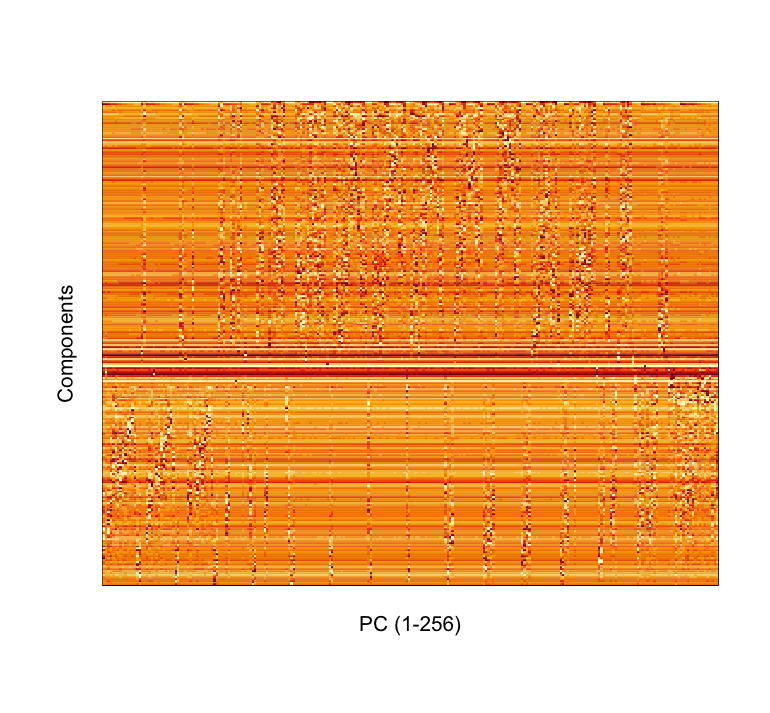
やっぱ、列ベクトルのヒートマップだけ見ても、よくわからないね。

そこで、PC1成分を棒グラフにしてみる。

head(pcaScore0)[,1:5]
#             PC1       PC2       PC3       PC4       PC5
#[1,] 0.005025779 0.3398974 0.4935447 0.4058873 0.5197696
#[2,] 0.008690831 0.3587962 0.4509923 0.4067744 0.5419167
#[3,] 0.005027335 0.3758440 0.4763016 0.4124084 0.5325050
#[4,] 0.060633086 0.4827584 0.5593437 0.3978971 0.5162717
#[5,] 0.074997179 0.4918104 0.4533958 0.3952488 0.5143074
#[6,] 0.075153602 0.5043891 0.4422169 0.3571957 0.5133769

#PC1の棒グラフ
barplot(pcaScore0[,1])
#quartz.save("Img07_pcaScore0.png", type="png", dpi=100); dev.off()

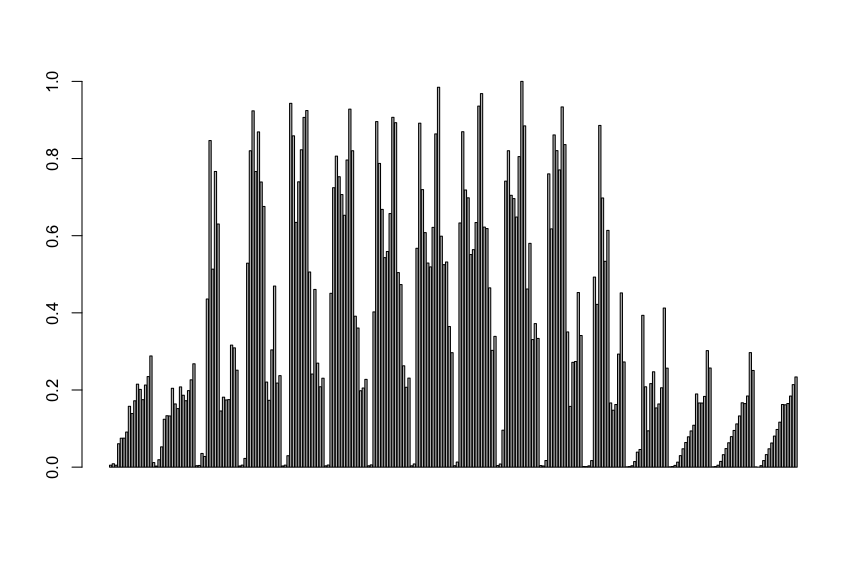
こっちの方がまだ分かりやすい。 ただ、何の成分が影響するかはイマイチ分からない。

「主成分と変数との相関係数」である因子負荷量(factor loading)の計算と可視化

#EBImageのロード
library(EBImage); options(EBImage.display = "raster")

#因子負荷量(factor loading) or 主成分負荷量(principal component loading): 
#計算方法: 固有ベクトル（result$rotation）と対応した固有値の平方根（result$sdev）との積をとる
pca01 <- sweep(x=pca$rotation, MARGIN=2, STATS=pca$sdev, FUN="*")

#第25主成分までの結果を可視化する
par(mfrow = c(5, 5), mai = c(0.1, 0.05, 0.1, 0.05))
for(N in 1:25){
b <- EBImage::Image(array(pca01[,N], dim=c(k, k, 3)), colormode = "Color")
EBImage::display(b) 
text(x = 5, y = 10, label = paste0("PC", N), adj = c(0,0), col = "white", cex = 1)
}
#quartz.save("Img08.png", type="png", dpi=100); dev.off()

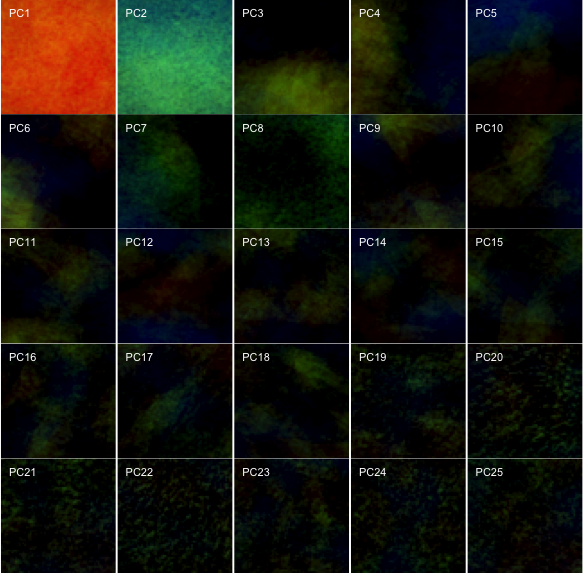
主成分負荷量まで計算して、二次元にマップする。 画像の特徴が何だかそれっぽく見えてくる。

画像データの復元

まずは、全データでのPCAの逆計算を行う。

#相関行列PCAの逆計算
pca00 <- t(t(pca$x %*% t(pca$rotation)) * pca$scale + pca$center)

#元データ
head(round(ImgDatCrop, 4))[c(1:5),c(1:5)]
#       [,1]   [,2]   [,3]   [,4]   [,5]
#[1,] 0.0039 0.0061 0.0069 0.0007 0.0026
#[2,] 0.0239 0.0267 0.0275 0.0235 0.0224
#[3,] 0.0032 0.0000 0.0000 0.0000 0.0000
#[4,] 0.0575 0.0531 0.0504 0.0474 0.0370
#[5,] 0.1019 0.1019 0.1020 0.1020 0.1020

#逆計算の結果
head(round(pca00, 4))[c(1:5),c(1:5)]
#       [,1]   [,2]   [,3]   [,4]   [,5]
#[1,] 0.0039 0.0061 0.0069 0.0007 0.0026
#[2,] 0.0239 0.0267 0.0275 0.0235 0.0224
#[3,] 0.0032 0.0000 0.0000 0.0000 0.0000
#[4,] 0.0575 0.0531 0.0504 0.0474 0.0370
#[5,] 0.1019 0.1019 0.1020 0.1020 0.1020

#一致数
table(round(ImgDatCrop, 4) == round(pca00, 4))
#  FALSE    TRUE 
#      3 3145725

元データと逆計算の結果は、少し誤差が出るみたいだけど、ほぼほぼ一致した。

ここで、%*%の演算子は、行列の積を求める。

続いて、第1主成分のみ、第1〜5主成分、第1〜10主成分、第1〜25主成分を使って 画像の圧縮を行い、復元画像の結果を可視化する。

第1主成分のみ

主成分スコア pca$xの対象列以外（はじめは、第1主成分以外）をゼロにして、PCAの逆計算を行う。

#第1主成分のみ
pcaP <- pca
pcaP$x[,-c(1)] <- 0

#相関行列PCAの逆計算
pca01 <- t(t(pcaP$x %*% t(pcaP$rotation)) * pcaP$scale + pcaP$center)

#クロップ画像の表示
par(mfcol = c(length(m1), length(m2)), mai = c(0.1, 0.1, 0.1, 0.1))
for(n in 1:p0){
a <- EBImage::Image(array(pca01[n,], dim=c(k, k, 3)), colormode = "Color")
EBImage::display(a)  
}
#quartz.save("Img09_PCA.png", type="png", dpi=100); dev.off()

第1-5主成分

#第1-5主成分
pcaP <- pca
pcaP$x[,-c(1:5)] <- 0

#相関行列PCAの逆計算
pca01 <- t(t(pcaP$x %*% t(pcaP$rotation)) * pcaP$scale + pcaP$center)

#クロップ画像の表示
par(mfcol = c(length(m1), length(m2)), mai = c(0.1, 0.1, 0.1, 0.1))
for(n in 1:p0){
a <- EBImage::Image(array(pca01[n,], dim=c(k, k, 3)), colormode = "Color")
EBImage::display(a)  
}
#quartz.save("Img10_PCA.png", type="png", dpi=100); dev.off()

第1-10主成分

#第1-10主成分
pcaP <- pca
pcaP$x[,-c(1:10)] <- 0

#相関行列PCAの逆計算
pca01 <- t(t(pcaP$x %*% t(pcaP$rotation)) * pcaP$scale + pcaP$center)

#クロップ画像の表示
par(mfcol = c(length(m1), length(m2)), mai = c(0.1, 0.1, 0.1, 0.1))
for(n in 1:p0){
a <- EBImage::Image(array(pca01[n,], dim=c(k, k, 3)), colormode = "Color")
EBImage::display(a)  
}
#quartz.save("Img11_PCA.png", type="png", dpi=100); dev.off()

第1-25主成分

#第1-25主成分
pcaP <- pca
pcaP$x[,-c(1:25)] <- 0

#相関行列PCAの逆計算
pca01 <- t(t(pcaP$x %*% t(pcaP$rotation)) * pcaP$scale + pcaP$center)

#クロップ画像の表示
par(mfcol = c(length(m1), length(m2)), mai = c(0.1, 0.1, 0.1, 0.1))
for(n in 1:p0){
a <- EBImage::Image(array(pca01[n,], dim=c(k, k, 3)), colormode = "Color")
EBImage::display(a)  
}
#quartz.save("Img12_PCA.png", type="png", dpi=100); dev.off()

次元圧縮のアニメーション

最後に、主成分数を変えて、計算結果の画像をアニメーションにしてみた。

library(EBImage); options(EBImage.display = "raster")
install.packages("animation"); library(animation)

#主成分数
Num <- 100

#アニメーション作成
animation::saveGIF({
for(m in 1:Num){

#主成分の絞り込み
pcaP <- pca
pcaP$x[,-c(1:m)] <- 0

#相関行列PCAの逆計算
pca01 <- t(t(pcaP$x %*% t(pcaP$rotation)) * pcaP$scale + pcaP$center)

#図示
par(mfcol = c(length(m1), length(m2)), family="HiraKakuProN-W3", 
    omi=c(0.1, 0.1, 0.5, 0.1), mai = c(0.1, 0.1, 0.1, 0.1))
for(n in 1:p0){
a <- EBImage::Image(array(pca01[n,], dim=c(k, k, 3)), colormode = "Color")
EBImage::display(a)
if(n == 1){
mtext(side = 3, line=1, outer=T, text = paste0("PC", m, "までを用いる。"), cex=1.25)
}}
}},  movie.name = paste0("Img13_PCA.gif"), interval = 0.5, dpi=100,
nmax = length(Num), ani.width = 500, ani.height=500, ani.type="png")

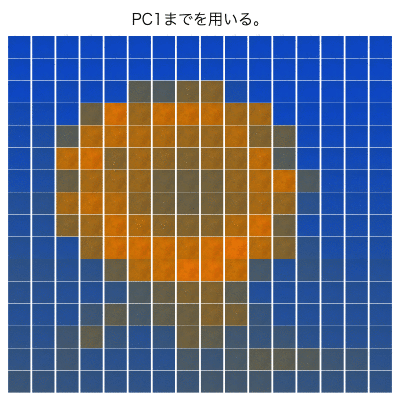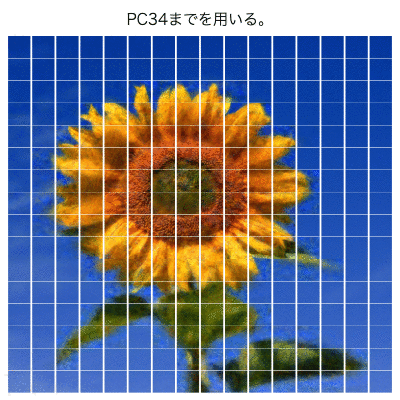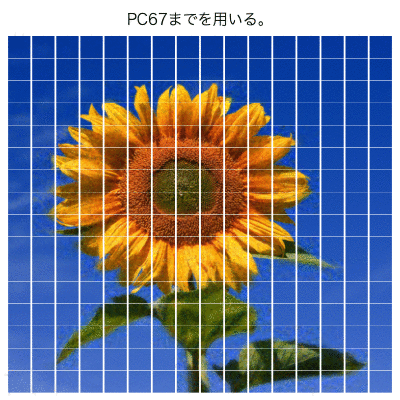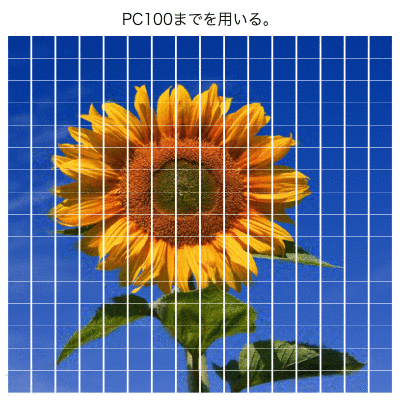
PC50くらいまでを使ったら、 ヒマワリ部分はほぼ再現できているように見える。

実行・生成に、結構時間がかかる。。

まとめ

画像データのPCA逆計算による画像圧縮を扱った。

PCAは様々なデータで応用できるのでホント奥が深い。

補足

分散共分散行列PCAの場合の逆計算

#Q-mode PCA: 分散共分散行列
pcaF <- prcomp(ImgDatCrop, scale = FALSE)

#分散共分散行列PCAの逆計算
t(t(pcaF$x %*% t(pcaF$rotation)) + pcaF$center)

既に作成したPCAモデルを用いた次元圧縮

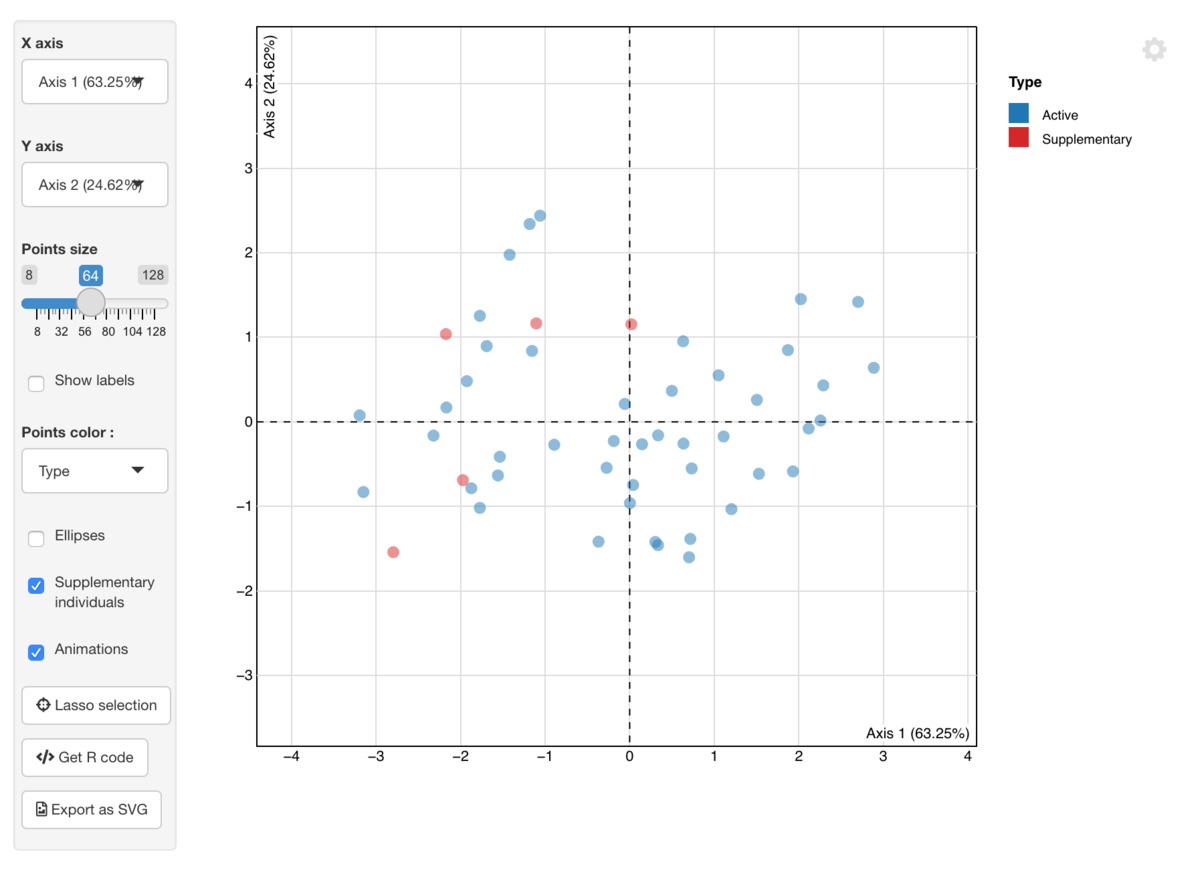
ここでは、新たなデータセットに対して、既に作成したPCAモデルを用いて次元圧縮を行う実施例を紹介する。

library(explor)
data(USArrests)

#PCA
pca_test <- prcomp(USArrests[6:50,], scale. = TRUE)
pca_test$supi <- predict(pca_test, USArrests[1:5,])

#可視化
explor(pca_test)

参考資料

メイン

http://racco.mikeneko.jp/Kougi/2016a/IPPR/2016a_ippr07_slide_ho.pdf

http://www.cfme.chiba-u.jp/~haneishi/class/2009/20091118.pdf

stackoverflow.com

サブ

http://manabukano.brilliant-future.net/document/text-PCA.pdfmanabukano.brilliant-future.net

stackoverflow.com

https://statistics.co.jp/reference/software_R/statR_9_principal.pdfstatistics.co.jp

https://data-science.gr.jp/implementation/ida_r_pca.htmldata-science.gr.jp

blog.statsbeginner.net

cran.r-project.org

stackoverflow.com

www.h.chiba-u.jp

https://data-science.gr.jp/implementation/ida_r_pca.htmldata-science.gr.jp

www.r-graph-gallery.com

webbeginner.hatenablog.com

www.nikkei-r.co.jp

*1:主成分分析には、応用分野によって様々な呼び名がある。信号処理の分野では、主成分分析のことを「KL変換」と呼ぶらしい。