【R言語/速度論/数値計算】１０倍量のヨーグルトを作りながら、乳酸菌の増殖曲線を考えてみた件

この記事は、2020年6月13日記事のアップデート版です。

はじめに
方法 (1): １０倍量ヨーグルト作製のマテリアル
方法 (2): １０倍量ヨーグルトの作製プロトコール
結果: 種菌の増殖曲線の検討
まとめ
- 参考文献

はじめに

最近、ヨーグルト作りにハマっています。

ヨーグルト菌、いわゆる、0.1Lの飲むヨーグルトから、１０倍量（1L）のヨーグルトを作っています。飲むヨーグルト１本は、だいたい１００円くらいなので、１０倍量で１０００円となって、必要経費を引いても、だいたい７００円弱お得になります。。また、ヨーグルトの酸味や固さを自分の好みの具合に調整できます。

今回、「ガセリ菌を使った１０倍量（1L）ヨーグルトの作製法」と「菌の増殖曲線」について検討したことを、それを実験ぽく紹介することにします*1。

方法 (1): １０倍量ヨーグルト作製のマテリアル

ガセリ菌の種菌（= 某メグミルク製のガセリ菌ＳＰ株の飲むヨーグルト）
培地（= 某メグミルク製の牛乳）
グルコース（= 三温糖）
1L プラビーカー（= ヨーグルトメーカーの容器）
スパチュラ（いわゆる、スプーンてやつ）
温度・時間可変の恒温器（いわゆる、ヨーグルトメーカー）

アイリスオーヤマヨーグルトメーカー甘酒メーカー飲むヨーグルトモードレシピブック付きメーカー保証付き温度調節機能付き IYM-013

アイリスオーヤマ(IRIS OHYAMA)

Amazon

方法 (2): １０倍量ヨーグルトの作製プロトコール

１. 1L プラビーカーに対して、スパチュラ（いわゆる、スプーンですね）3-4杯分のグルコース（要するに、砂糖です）を添加します。おおよそ、15-20gくらい加えます。

２. ガセリ菌の種菌を全量加えて、振盪混合します（いわゆる、振って混ぜます）。

３. 培地（いわゆる、牛乳です）で、1L目盛までメスアップします（つまりは、牛乳を900mL入れる）。

４. 蓋を軽めに閉めて、３５℃の恒温器（いわゆる、ヨーグルトメーカー）内で静置します。オーバーナイト・インキュベート（一晩培養）します。

ガセリ菌の場合、だいたい、12-15時間ほどインキュベートすると、良い感じの固形ヨーグルトが出来あがります。

５. ４℃で保管して（冷蔵庫で保管）して置いておきます。そして、官能評価を行います。いわゆる、「食う」というやつです。

結果: 種菌の増殖曲線の検討

微生物の増殖曲線について調べてみると、 ゴンペルツの増殖曲線 (Gompertz growth curve)というのがあるようです。

もともと、１８３２年に、Benjamin Gompertz によって、人間の死亡率を推定するためのモデル式として、「ゴンペルツ関数（Gompertz function）」が提案されたことを起源としているようです。

Gompertz, B. "On the Nature of the Function Expressive of the Law of Human Mortality, and on a New Mode of Determining the Value of Life Contingencies." Phil. Trans. Roy. Soc. London 123, 513-585, 1832.

それから、さらに１００年後、１９３２年に、Charles Winsorによって、微生物の成長過程を説明するための方程式として使用されたようです。

www.pisces-conservation.com

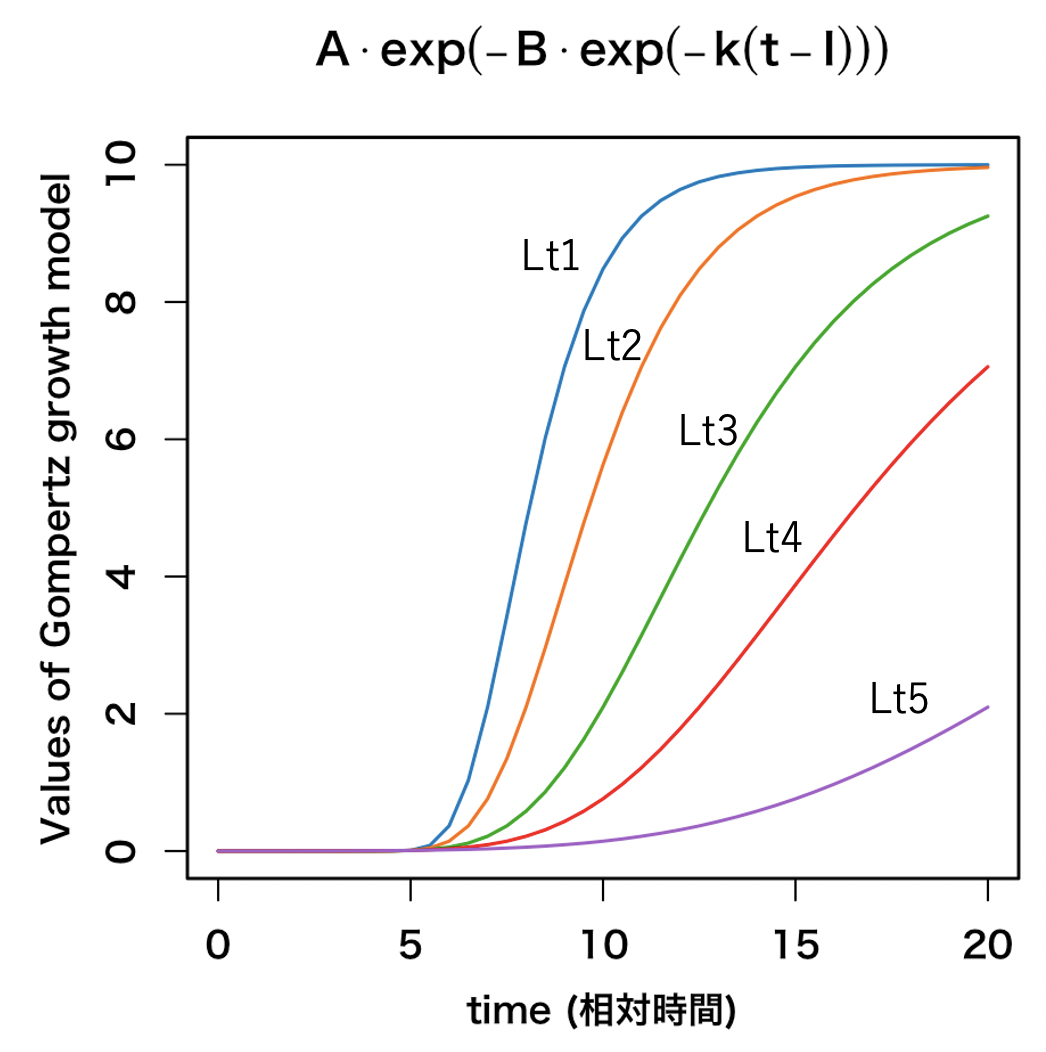
ゴンペルツの増殖曲線の一般式は、以下のように定義されます。

$A \cdot exp(-B \cdot exp(-k (t - I)))$

このとき、

A は、飽和（上限）時の値, A > 0

B, k は、成長速度係数 (Growth velocity factor), k > 0, B > 0

I は、変曲点

t は、相対時間

をそれぞれ意味します。

今回、この増殖曲線について、成長速度係数 k を、0.75、0.5、0.3、0.2、0.1 の５パターンに設定して、 R上で数値計算のシミュレーションしてみました。

## 固定パラメータの設定
# A: 飽和（上限）時の値, A > 0 
A <- 10
# B: 成長速度係数, B > 0
B <- 7
# I: 変曲点
I <- 5
# t: 相対時間
t <- seq(0, 20, 0.5)

## パラメータ k の設定
# 成長速度係数 k = 0.75
k1 <- 0.75
Lt1 <- round(A*exp(-B*exp(-k1*(t-I))), 3)

# 成長速度係数 k = 0.5
k2 <- 0.5
Lt2 <- round(A*exp(-B*exp(-k2*(t-I))), 3)

# 成長速度係数 k = 0.3
k3 <- 0.3
Lt3 <- round(A*exp(-B*exp(-k3*(t-I))), 3)

# 成長速度係数 k = 0.2
k4 <- 0.2
Lt4 <- round(A*exp(-B*exp(-k4*(t-I))), 3)

# 成長速度係数 k = 0.1
k5 <- 0.1
Lt5 <- round(A*exp(-B*exp(-k5*(t-I))), 3)

## データフレームに変換
Data <- data.frame(t, Lt1, Lt2, Lt3, Lt4, Lt5)

par(family="HiraKakuProN-W6", lwd=1.5, 
    cex=1, mgp=c(2.5, 1, 0), mai=c(0.75, 0.75, 0.8, 0.25))
plot(Data$t, Data$Lt1, type="l", col="#0078B9",
     main=expression(A %.% exp(-B %.% exp(-k*(t - I)))),
     xlab="time (相対時間)",ylab="Values of Gompertz growth model")
points(Data$t, Data$Lt2, type="l", col="#FF7700")
points(Data$t, Data$Lt3, type="l", col="#00A400")
points(Data$t, Data$Lt4, type="l", col="#E90017")
points(Data$t, Data$Lt5, type="l", col="#9D62C3")

ゴンペルツ増殖曲線の作図

さらに、plotlyパッケージを用いて、増殖曲線を可視化しました*2。

if(!require("plotly")){install.packages("plotly")}; library(plotly)
fig <- plot_ly(Data, x = ~t)
fig <- fig %>% add_trace(y = ~Lt1, name = 'Lt1', mode = 'lines')
fig <- fig %>% add_trace(y = ~Lt2, name = 'Lt2', mode = 'lines')
fig <- fig %>% add_trace(y = ~Lt3, name = 'Lt3', mode = 'lines')
fig <- fig %>% add_trace(y = ~Lt4, name = 'Lt4', mode = 'lines')
fig <- fig %>% add_trace(y = ~Lt5, name = 'Lt5', mode = 'lines')
fig <- fig %>% layout(xaxis = list(title = 'time'),
                      yaxis = list(title = 'Values of Gompertz growth model'))
fig