【R言語で作成するアニメーション】データ分布のアニメーション〜正規分布編〜

正規分布に従うデータのアニメーション
実行したスクリプト
補足

正規分布に従うデータのアニメーション

正規分布に従うデータ（乱数）を、異なるサンプルサイズで準備して、それらデータについて、ヒストグラム・密度分布、累積分布、Q-Qプロットとかで可視化して、アニメーションにもしてみた。

以下のアニメーションを作成した。

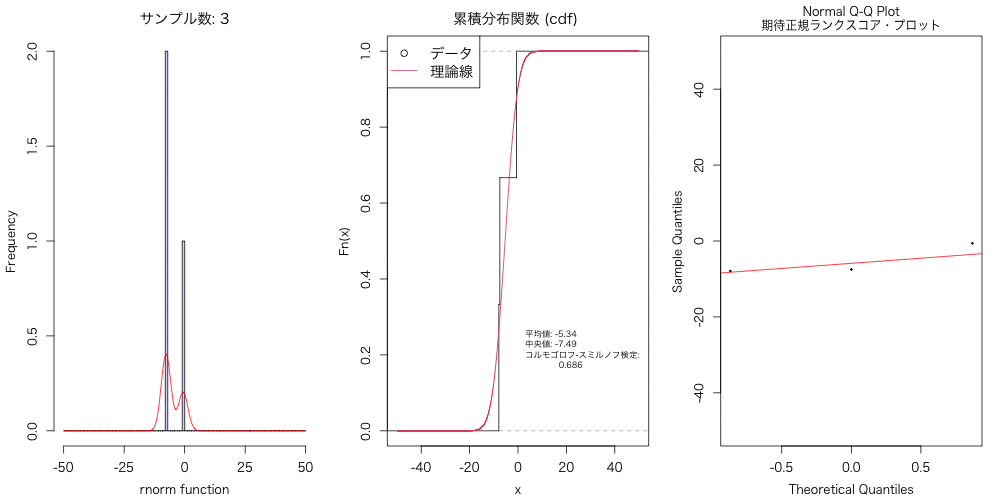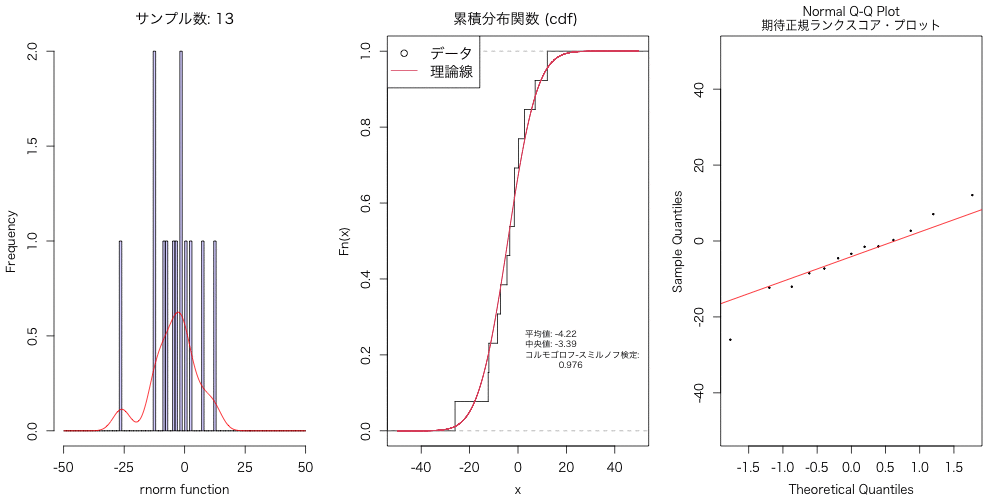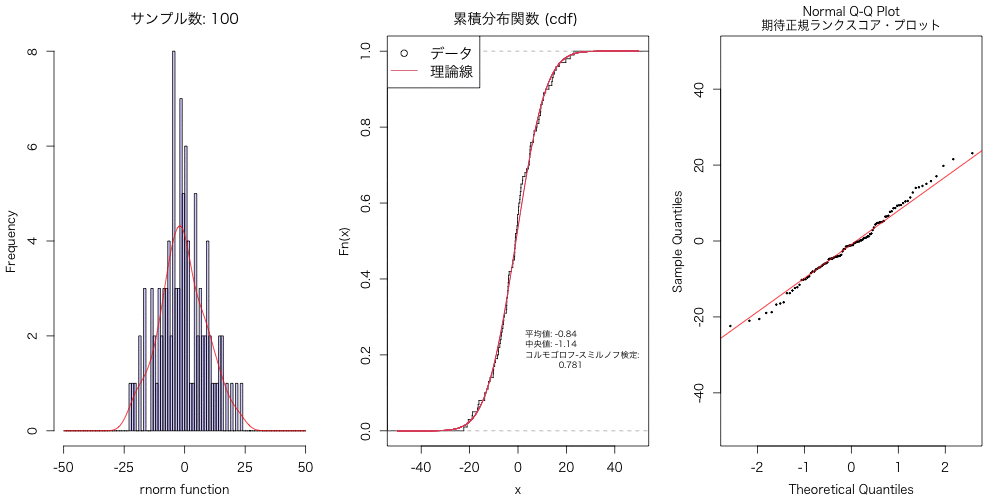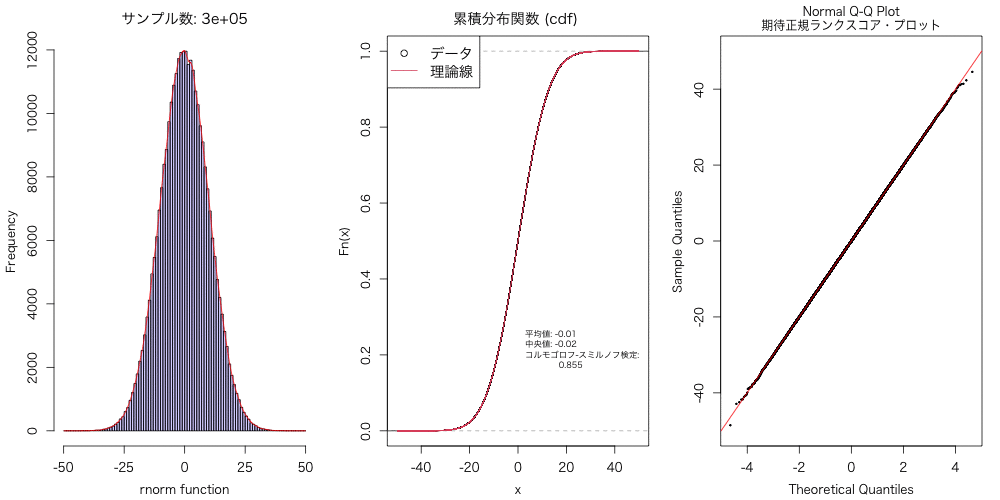
実験的に、こういうのを試すと、データ分布は数千〜数万はないと、正規分布には近似しないよねということに気づかされる。

実行したスクリプト

まずは、必要なパッケージをインストールする。

install.packages("animation")

library(animation)

そして、サンプルサイズの数値を、３〜300000までの数値ベクトルにて作成する。

Num <- c(3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 17, 20, 
         25, 30, 40, 50, 75, 100, 300, 500, 1000, 3000, 5000, 
         10000, 30000, 50000, 100000, 300000)

次に、「animation::saveGIFとfor-ループ」を組み合わせて、プロットの可視化結果をGIFアニメーションに変換する。

animation::saveGIF({
for(n in Num){

#プロット設定
par(mfrow = c(1,3), family="HiraKakuProN-W3",
    cex=1, mgp=c(2.5, 1, 0), mai=c(0.75, 0.75, 0.5, 0.25))

#正規分布に従う乱数を n 個生成
a <- rnorm(n, mean = 0, sd = 10)

#データ分布のヒストグラム
hist(a, breaks=seq(-50, 50, by=1), main=paste0("サンプル数: ", n),
     xlab="rnorm function", col=rainbow(10, alpha = 0.2)[8], xaxt='n')
#X軸ラベルの書き直し
axis(side=1, at=seq(-50, 50, 25), labels=seq(-50, 50, 25))

#密度分布
b <- density(a, kernel = "gaussian", n = 512, from=-50, to=50)
lines(b$x, b$y*n, col="red")

#経験的分布関数
d <- ecdf(a)
plot(d, do.point=F, verticals=T, xlim=c(-50, 50),
     main="累積分布関数 (cdf) ")

#正規分布時の理論式の追加
x <- seq(-50, 50, 0.01)
lines(x, pnorm(x, mean=mean(a), sd=sqrt(var(a))), col=2)

#データ分布の平均値、中央値、コルモゴロフ-スミルノフ検定
text(0, 0.2, cex=0.7, pos=4,
     labels=paste0("平均値: ", round(mean(a), 2), "\n",
                   "中央値: ", round(median(a), 2), "\n",
                   "コルモゴロフ-スミルノフ検定: \n            ", 
                   round(ks.test(a, "pnorm", mean=mean(a), sd=sd(a), alternative = "two.sided")$p.value, 3)))
legend("topleft", legend=c("データ", "理論線"), cex=1.2,
       pch=c(21, NA), lty=c(NA, 1), col=c(1, 2))

#Q-Q プロット
qqnorm(a, cex=0.25, cex.main=1, 
       ylim=c(-50,50),
       main="Normal Q-Q Plot\n期待正規ランクスコア・プロット")
qqline(a, col="red")
}},  movie.name = paste0("Animation.gif"), interval = 1, dpi=400,
nmax = length(Num), ani.width = 1000, ani.height=500, ani.type="png")